(Это одна из главок из моей книжки, посвященных музыкальным строям народов мира. Наряду с индийским, пифагорейским, китайским и другими. Одна из. Относящаяся к Европе. И Америке. И России. К сегодняшнему времени. К другому – нет, не относящаяся.)
После победного шествия пифагорейского строя по Греции и Италии музыка, да и все остальные виды искусства в Европе пришли в упадок. В Vм веке нашей эры Римская империя окончательно рухнула, добро победило зло, положив конец бесчинствам римских императоров и Европа на 1000 лет погрузилась в мрачное средневековье. Все, что можно было разграбить, было разграблено, все, что можно было потерять, было потеряно. Примерно 1000 лет никто сильно не задумывался, насколько гармонично и правильно настроены музыкальные инструменты.
Впрочем, это не совсем так. В мрачное средневековье успешно развивалась арабская культура, подарив нам арабские цифры, алгебру, алхимию и алкоголь. А также и все остальные слова на «аль». В арабском мире, в том числе и в Кордобском каганате, огромной части современной Испании, успешно развивалось музыкальное творчество. Был рожден уникальный звукоряд, содержащий 17ть и более нот в одной октаве. Он тоже основывался на традициях Пифагора. Авиценна, Абу Али Хусейн ибн Абдаллах ибн Сина (980-1037), более известный у нас как медик, был еще и теоретиком музыки. К сожалению, в эту книжку я не включил раздел «арабский музыкальный строй» (также, как и яванский, сиамский, древнееврейский и т.д.), просто в силу недостатка времени и слабых познаний в истории этих культур. Хотя, может быть через некоторое время я опубликую какую-то работу на тему связи Каббалы с музыкой. Хотя сейчас изучением Каббалы занимается даже «Мадонна», постараюсь придерживаться только циферек, не вдаваясь в религиозные концепции.
Итак, что было в Европе? В основном в средние века использовались струнные безладовые инструменты. Математическая точность настройки для них не требовалась. Каждый музыкант мог подкорректировать высоту звука самостоятельно.
-
«Зачем ты хочешь петь терцию?! Иди лучше поспи! Или поешь. А еще лучше – вначале поешь, потом поспи!»
-
Что же делать?
- - -
Спор, как мы понимаем, был конструктивен. Попробуем, как Гордий или Герострат или Гекельберри Финн, разобраться в этой проблеме.
Когда хористы пытались петь терцию до-ми, они интуитивно старались петь наиболее консонансный интервал, похожий на большую терцию. Такой интервал получается естественным образом из гармоник свободно звучащей струны, из «натурального звукоряда» (см. про натуральный строй ниже). Отношение частот ми и до в этом строе равно 5/4, этот интервал еще называется «чистой терцией». Действительно, по Пифагору, самые чистые и благозвучные интервалы получаются при отношении частот звуков (длин струн) как небольшие целые числа. Уна 1/1, октава 2/1 вообще считаются абсолютно консонансными интервалами (хотя, как мы помним, высшие гармоники и обертоны реальных звуков диссонируют между собой, то есть абсолютного консонанса просто не существует), интервалы с соотношением частот 3/2 и 4/3, чистые квинта и кварта тоже звучат замечательно. Можно предположить, что интервал с отношением частот 5/4 тоже будет благозвучен. Вот и хористы стремились петь вместо пифагорейской терции, где соотношение частот нот Ми-До равно 81/64, чистую терцию, с соотношением частот 5/4. Как мы понимаем, 81/64 не равно 5/4, это отличие было названо «дидимовой коммой». «Дидимова комма» наряду с «пифагоровой коммой» были обнаружены и яростно обсуждались еще самими пифагорейцами, доходило до драк.
Хорошо, раз так настаивали хористы, музыкальные теоретики согласились на то, чтобы заменить пифагорейскую «нечистую» большую терцию До-Ми на «чистую». Но тут стало возникать множество дополнительных проблем. Может быть пифагорейский строй был и не хорош, но он определял каждую ноту звукоряда единственным образом. Теперь же, каждую ноту музыкального строя можно было получить не только с помощью квинт и октав, а еще и с помощью чистых терций. То есть, вместо одной ноты у нас получалось целая группа нот с одним названием. И если на хористов еще можно было махнуть рукой, то на органистов махать руками не следовало, за ними стояло духовенство и большие деньги. Да и вообще, представьте себе орган с множеством труб почти одинаковой длины, с множеством клавиш, соответствующих одной ноте. Можно сойти с ума. Органисты молча, мрачно спивались.
Какое-то время, довольно долгое, такой музыкальный строй, содержащий кроме чистых квинт еще и чистые терции, существовал. Он получил название «чистого строя» (англ. just intonation, pure intonation). Разработку чистого строя обычно связывают с именем итальянского композитора и музыкального теоретика Джозеффе Царлино (1517-1590). Можно представить, сколько «лестных» слов Царлино слышал в свой адрес!
Однако, чистый строй впервые позволил использовать мажорные и минорные гармонические аккорды (трезвучия) при игре на инструментах с фиксированной частотой звуков (органах, клавикордах, клавесинах). Это было в некотором смысле прорывом. Народ в костелах, стуча тяжелыми железными сапогами о шершавый гранитный пол, требовал минорных и мажорных трезвучий, исполняемых на органе. И народ их получил. Народ стал счастлив.
Но, бесплатных пирожных, как мы помним, не бывает. За счастье народа приходилось платить нечистой совестью и отсутствием гармонии в душе. А также в музыке. Возникло по крайней мере две проблемы.
Во-первых, как я уже упоминал выше, каждую ноту теперь можно было построить множеством различных способов – вернее, можно было построить множество «вариантов» одной и той же ноты. Музыкальный строй при этом по-прежнему остается незамкнутым (то есть «возвращение» к той же ноте при прохождении по октаво-квинтовому кругу по-прежнему невозможно). Более того, различные гармонические «роли» одной и той же ноты теперь обладали разными частотами. Музыкант при музицировании был фактически «привязан» к одной тональности. Модуляции и отклонения в другие, даже ближайшие, тональности становились невозможны, так как в них инструмент оказывался «настроен не идеально». Например, настроив орган для игры в чистом строе ноты «до» органист не мог уже перейти в тональность «ре», так как в этой тональности квинта тонического трезвучия, которая встречается довольно часто, оказывалась «волчьей квинтой», то есть квинтой с большой ошибкой, она звучало очень диссонансно. То есть, формально, органист мог играть полифонию, но, фактически он мог ее играть только в одной тональности. Переход даже в ближайшие и родственные тональности был невозможен. Органисты чувствовали себя связанными по рукам и ногам. Вечерами они много пили. Иногда начинали прямо с утра.
Во-вторых, такое количество «похожих», но разных нот (около 85 в октаве) делало очень сложным игру и само создание музыкальных инструментов. Ведь, по-хорошему, речь идет не об одном «чистом строе», а о целой совокупности «чистых строев», по одному для каждой тональности. Посочувствуем средневековым органистам, фирмам-производителям органов и настройщикам. (В этом месте должна была быть реклама фирмы-производителя органов!)
Итак, мы поняли, что «чистый» строй несовершенен. Однако, он достоин некоторого внимания к себе.
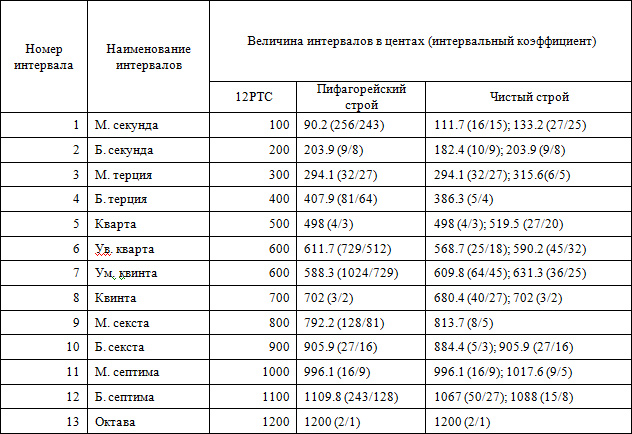
Диатоническая мажорная гамма «чистого» и пифагорейского строя в интервальных коэффициентах выглядит так:
Даже на таком простом примере мы видим проблемы с «чистым строем». Одинаковые по названию интервалы имеют разную величину. Например, квинты на 1, 3, 4, 5 и 6-й ступенях соответствуют отношению 2/3, а на 2й ступени – 27/40 (3/5:8/9 = 27/40). Малые терции на 3, 6-й и 7-й ступенях имеют интервальный коэффициент 5/6, а такой же интервал, отложенный от 2й ступени - 27/32 (3/4:8/9=27/32). Короче говоря – и здесь нет гармонии!
Как пишет замечательный музыкант, математик, изготовитель музыкальных инструментов, настроенных по «совершенным консонансам» Крис Форстер в своей книге «Музыкальная математика», проблемы с музыкальными строями начались только при начале использования инструментов с фиксированной настройкой – органов, клавикордов и др. Если музыкант играет на безладовом струнном инструменте, он с легкостью может обойти эти Сциллы и Харибды «чистого строя», да и любого другого строя. Просто, чуть смести пальчик вбок – и нет проблемы, чуть подтяни колок – и наступит небесная гармония. Не зря же, индийские музыканты, у которых один из самых сложных и самых точных с точки зрения математики и психоакустики музыкальный строй, стараются использовать безладовые инструменты типа сарод, или ладовые, но с очень большой гибкостью по высоте «фиксированных порожком» звуков – типа ситар. И у них нет проблем, нет волчьих квинт. Правда, у них нет и полифонии в европейском смысле этого слова. Ладно, не будем ругать европейцев, посмотрим как они выкручивались.
Итак, осталось два основных типа музыкальных инструментов: органы, они были были чрезвычайно усложнены. И безладовые струнные, прообразы наших виолончелей и скрипок. Музыкальные теоретики зашли в тупик. Настроить музыкальный инструмент «совершенным образом» у них не получалось.
Тогда вышли на арену математики. Они сказали: «Сейчас, мы со всем этим безобразием разберемся!» Попытки сделать совершенный музыкальный строй предпринимали такие математические мэтры, как Кеплер, Декарт, Лейбниц, Эйлер. О теории гармонии Эйлера шутливо говорили, что она слишком музыкальна для математиков и слишком математична для музыкантов. Но, тем не менее, математики быстро выяснили, что построить универсальный строй и одновременно сохранить чистоту базовых интервалов ни теоретически, ни практически невозможно. Можно только распределить ошибку, расхождение между нашими представлениями о гармоничности, консонанстности музыкальных интервалах и суровой реальностью более-менее равномерно по музыкальной гамме. То есть начались попытки создания темперированных, то есть «равномерных» музыкальных строев.
Изобретателем современного равномерно-темперированного 12ти нотного строя следует считать китайца. Звали его Чжу Цзай Юя (р.1536), он был принцем династии Мин, имевшим страсть к занятиям музыкой, математикой и астрономией. После приблизительно тридцати двух лет и восьми (или девяти) месяцев тщательного изучения и экспериментирования им была разработана математическая основа построения равномерно темперированного музыкального строя. Для длины струны и флейты он предлагал ряд чисел, равных корню двенадцатой степени из двух, а для диаметра флейты – корню двадцатьчетвертой степени из двух. После того как Чжу Цзай Юй опубликовал свое изобретение в 1584 г., не китайцы (которые считали его строй «нечистым»), а европейцы обратили на него внимание.

Настройка инструмента чжунь по теории Чжу Цзай Юя. Рисунок из трактата 1584 г. Справа - инструмент спереди, слева - задняя сторона инструмента.
Это было время, когда налаживался контакт между Китаем и Европой, и, видимо, каким-то образом идея равномерной темперации проникла на Запад. Первое упоминание о ней появилось в неопубликованных бумагах математика Симона Стевина (1548-1620). В 1636 г. сведения о равномерной темперации были изданы французским монахом-миноритом, теологом, физиком и музыкальным теоретиком Мареном Мерсенном (1588-1648) в его книге под названием «Всеобщая гармония». К концу века темперированный строй исследовал немецкий музыкальный теоретик и акустик Андреас Веркмейстер (1645-1706), которому часто и приписывается его изобретение, а в 1722 г. публикуется эпохальная работа И.С. Баха «Хорошо темперированный клавир». Тут важно подчеркнуть, что понятие «хорошая темперация» во времена Баха совсем не подразумевало равномерную темперацию в современном понимании. В ходу было целое семейство неравномерных темпераций позволявших более-менее успешно играть в любой из тональностей. Вот бы послушать произведения Баха на тех инструментах, на которых он сам играл! Эх!
Итак, новый 12ти нотный равномерно-темперированный строй родился. У нового строя было много оппонентов. Новый строй нарушал строгую пропорцию интервалов, и, как следствие, в аккордах начали появляться небольшие биения. Я об этом кратко писал в разделе «Относительный музыкальный слух», все дети прекрасно слышат эти биения. В глазах многих теоретиков наличие биений в чистых интервалах и аккордах было посягательством на чистоту музыки. Андреас Веркмейстер утверждал, что в новом строе все тональности становились однообразными и симметричными, в то время как в старых строях из-за неравномерности темперации каждая тональность имела свое неповторимое звучание. А народу было все равно, он ликовал и не мучился мучительными муками.
Стоит напомнить, что к этому моменту уже были опубликованы основные работы по теории логарифмов, поэтому темперированный строй воспринимался как настоящий триумф прогресса, в первую очередь, математики. Ведь схема построения современной темперации построена по экспоненциально-логарифмическому принципу. Кто ничего не понял – не переживайте, это нормально.
Гении изменяют наш мир одним лишь своим существованием. Публикация «Хорошо Темперированного Клавира» положила начало распространению 12ти нотной равномерной темперации в мире. Равномерный темперированный строй был с ликованием, сопровождавшимся криками «Браво! Ты крут! Еще парочку!», принят теми, кто понимал практические преимущества такого строя. Ведь равномерная темперация позволяет легко совершать переход из тональности в тональность, транспонировать музыкальные произведения. С другой стороны, равномерная темперация всегда имела (и до сих пор имеет) большое количество противников, не без основания придающих большое значение чистоте тона. Не без основания. Но равномерная темперация одержала окончательную победу, заняв главенствующие положение в европейской музыке, начиная с 18-19 веков, теперь на ней основывается вся современная всеми нами любимая музыка. Особенно – популярная музыка. Попса. Особенно сильно любимая мной музыка. И сейчас, прямо сейчас я ее особенно сильно люблю, такое острое, резкое чувство любви.
Равномерно-темперированные строи (равномерные темперации)
Вернемся к истории создания 12ти нотного равномерно-темперированного строя в Европе. Китайское семя проникло в Европу и начало там расти и развиваться. Что же делали европейские музыкальные теоретики?
Многие из них, например, Веркмейстер и Нейдгардт, нашли, казалось бы, приемлемый путь разрешения проблемы «волчьих квинт» и помогли их последователям создать современный 12ти нотный равномерно-темперированный строй. Логика этого пути проста. Если разделить пифагорову комму (1/9 тона) на 12 равных частей, т. е. распределить ее между двенадцатью квинтами этого строя, то каждая квинта уменьшится на 1/108 тона (1/9:12=1/108). При этом условии двенадцатая квинта вверх от звука с (his) совпадает с октавой от того же звука «с». Совпадение his с «с» , a deses с «с» вызовет совпадение всех энгармонически равных звуков (нот с одним названием), отличающихся по высоте на пифагорову комму. Это совпадение произойдет путем небольшого смещения обоих звуков. Отличие чистой квинты от темперированной при этом будет около 1-2х центов, заметно на слух, но приемлемо. Вопрос только остается – для кого приемлемо? В пифагорейском строе все целые тоны получаются посредством двух квинтовых ходов и потому равны между собой, последовательность 6 целых тонов (от звука с) приводит к звуку his, который на 1/9 тона выше с, поэтому, уменьшая чистые квинты на 1/108 тона, мы уменьшаем каждый целый тон на 1/54, а последовательность 6 тонов на 1/9 тона (пифагорову комму). То есть, в рассматриваемом нами темперированном строе октава состоит из 6 равных целых тонов. В пифагорейском строе хроматический полутон (см. главу «Пифагорейский строй») больше диатонического, поэтому целый тон пифагорейского строя делится на два неравных полутона. В полученном нами темперированном строе хроматический полутон равен диатоническому. В этом строе любой целый тон делится на два равных полутона. Таким образом, в этом строе октава состоит из 12 равных полутонов, а все другие интервалы из меньшего количества этих одинаковых полутонов - от 11 (большая септима) до 1 (малая секунда). Посмотрим теперь насколько приемлемы новые интервалы в равномерно-темперированном строе с музыкальной, акустической точки зрения. Так как этот строй получается путем деления октавы на 12 равных полутонов, то все октавы этого строя, как и в прочих теоретических строях, чистые. Темперированная квинта, которая меньше чистой на 1/108 тона, и темперированная кварта, которая больше чистой на 1/108 тона, отличается от чистых интервалов на величину около 2х центов. Взрослый человек не чувствует диссонанса в этих интервалах, но слышит биения, хорошо слышат эти биения дети. Особенно – дети в возрасте 5 лет, 7 месяцев и 12 дней. Лучше, чтобы они были блондинами. Или блондинками. Темперированная большая терция меньше пифагорейской на 1/27 тона, больше чистой на 1/16 тона. Сравнивать с пифагорейской терцией, правда, довольно бессмысленно, ведь чистый строй придумали именно потому, что пифагорейские терции звучали диссонансно. Отличие «темперированной большой терции» от «чистой» составляет 1/16 тона или около 12 центов. Такое отличие очень заметно на слух, мы слышим сильные биения, вокалисты стараются не использовать эти интервалы. Вот почему в детстве терции мне казались очень диссонансными интервалами! Не прошло и 20ти-30ти лет, возникло понимание, пришла мудрость, но ушло здоровье и потерялся интерес к женщинам. Пробудился интерес к пиву, газетам и футболу. И к графомании и морализаторству.
Темперированная малая терция меньше чистой на 1/14 тона. Это тоже очень большое отличие, вызывает ясно слышимые биения. Такой интервал почти диссонансен. Большая и малые терции по благозвучности, консонасности заметно отличаются от чистых, но в полифонической, многоголосной музыке многими музыкантами и слушателями считаются приемлемыми. Соглашусь, куда же деваться то?
С диссонансными интервалами, малой и большой секундой, несколько проще. Они в любом строе звучат диссонансно. А уж больше или меньше – большой (или малой) разницы нет.
Несмотря на собственные исследования европейский музыкальных теоретиков, китайское семя оказалось сильнее.
В рамках 12ти нотного равномерно-темперированного строя, предложенного Чжу Цзай Юем, частота N-ной ноты 12ти нотной хроматической определяется формулой:
F(n) = корень "n"- ной степени из 2х, умноженный на F_0
где F_0 - частота начальной ноты звукоряда, хроматической гаммы, например, ноты «До».
В этом строе, также, как и в «веркмейcтеровском», темперированные квинты и кварты не слишком сильно отличаются от «чистых», а терции – сильно отличаются и звучат достаточно фальшиво (см. сравнительную таблицу в конце раздела).
Итак, наука победила разум и родила «нечистый», но «приемлемый» музыкальный строй. Возникла еще одна проблема. Придумать то его придумали, а вот как настроить в таком строе рояль, скажем? Ноутбуки и лэптопы в 17м веке еще были слишком громоздки, к тому же спектральные и гармонические анализаторы звука были весьма дороги и стоили больше, чем 2 бельгийские коровы. Как в такой ситуации поступали и поступают настройщики роялей, скажем?
Настройка хроматической гаммы 12-нотного равномерно-темперированного строя на практике представляет довольно большие трудности. Так как все интервалы этого строя можно получить посредством квинтовых ходов, то теоретически вопрос сводится к нахождению числа биений в секунду, которое дает темперированная квинта на различных ступенях хроматической гаммы РТС, практически же - к отсчету указанных биений настройщиком музыкальных инструментов.
Сейчас на практике, настройщики роялей не считают число биений на слух, а выставляют высоту каждой струны по электронному камертону. Настройка инструмента происходит значительно быстрее, но с точки зрения автора волшебство звука только что настроенного инструмента теряется. В чем тут дело – непонятно.
Мы помним из главы 1 «Звук», что у чистой квинты 3-я гармоника ее нижнего звука совпадает с 2-й гармоникой ее верхнего звука. В темперированной квинте указанные гармоники не совпадают, и между ними возникают биения (строго говоря, не только между ними, между высшими гармониками тоже). Для квинты с - g число биений в секунду равно 0,89, так как частота 3-й гармоники с равна 784,89, частота 2-й гармоники g равна 784. Число биений в секунду для квинты es - b равно 1,07, для квинты fis - сis - 1,25, а для квинты а - е равно 1,48. То есть, для настройки темперированных квинт необходимо найти числа биений для всех 12 квинт. На практике при настройке музыкальных инструментов с фиксированной частотой звуков (рояли, органы, шаманские бубны), на эти тонкости закрывают глаза, по этому признаку можно сразу определить настройщика – он ходит с закрытыми глазами. Обычно для всех 12 квинт берут среднее число биений, т. е. для квинт 1-й октавы 1,1 в секунду. Эта замена значительно упрощает процесс настройки темперированных квинт, хотя и вызывает некоторое расхождение между вычисленными интервалами 12-звукового равномерно-темперированного строя и фактически настраиваемыми. Хорошие настройщики роялей настраивают квинты на слух, не считая при этом каждый раз число биений. В случае наличия хорошего слуха и хорошего опыта настроить рояль можно хорошо.
Резюмируем. Я так долго ругал равномерно-темперированный строй, что сам начал забывать, что он довольно неплох, он был «выстрадан» поколениями музыкантов и математиков, желавших играть или слушать полифонию. Итак, вот основные плюсы РТС: 1) он представляет собой строй замкнутый и энгармонический (cis=des); 2) он состоит из интервалов, которые как при мелодическом, так и при гармоническом их воспроизведении вполне приемлемы для музыкального слуха, особенно в сложных музыкальных произведениях; 3) он имеет в октаве только двенадцать звуков, которые при этом могут выполнить несколько различных ладовых функций; 4) он требует сравнительно простого устройства многоголосных инструментов.
Хорошо, мы создали 12ти нотный равномерно-темперированный строй. Мы научились с помощью подсчета количества биений или с помощью электронных камертонов настраивать инструменты в соответствии с этим строем. Но почему мы должны использовать только 12ть нот? Наше ухо позволяет различать и гораздо более тонкие градации звуков по высоте. Появилось множество подходов, где октава делится не на 12, а на большее количество равных интервалов. Среди равномерных темпераций, в которых октава делится на большее количество частей, чем 12, можно назвать прежде всего 24-нотный равномерно-темперированный строй. Этот строй, сохраняющий все особенности 12-нотного равномерно-темперированного строя, дает возможность брать с большой точностью интервалы, в интервальных коэффициентах которых есть числа 11 и 13. Улучшение терций и секст (сравнительно с 12-звуковой темперацией) в рассматриваемой темперации не наблюдается, хотя это было бы неплохо. Ведь терции в 12ти нотном РТС самые «грязные», «не чистые», с большим количеством биений. Другая равномерная темперация, которая является просто расширением 12-нотного равномерно-темперированного строя, является 48-тотная равномерная темперация. В этом строе сохраняются все особенности как 12-звуковой, так и 24-звуковой равномерных темперации. Также там могут быть достаточно точно использоваться интервалы, коэффициенты которых включают в себе множитель 7. Кроме того, этот строй дает возможность получить терции и сексты, весьма близкие к натуральным. А вот это уже хорошо! Музыкальные инструменты с фиксированной частотой звуков, необходимые для музыкального использования этого строя, весьма сложны по своему устройству (48 звуков в октаве, практически «чистый музыкальный строй»!). Наиболее совершенная в звуковом отношении темперация была бы 53-звуковая, дающая возможность осуществить с большим приближением интервалы как чистого, так и натурального строя. «Гармониум» с 53 звуками в октаве был построен Бозанкетом. Практического применения рассматриваемая темперация не получила, что понятно. Те, кто любят чистые интервалы, могут слушать вокальные или скрипичные концерты, где эти интервалы употреблять просто, можно также слушать индийскую или китайскую музыку. Для людей, кто в меньшей степени любит чистоту интонаций, вполне подходит и современный 12-ти нотный РТС.
Для любителей дадим несколько более подробное описание важных для рождения современного 12ти нотного равномерно-темперированного музыкального строя звукорядов: Натурального и Среднетонового.
Благодарности и использованные материалы
Материалы Википедии,
6ти томной музыкальной энциклопедии,
Холопов Ю. Н. «Гармония. Теоретический курс»
В. Г. Порвенков "Акустика и настройка музыкальных инструментов"
Гарбузов H. A. «Зонная природа звуковысотного слуха»
Еремеев В. Е. «Символы и числа Книги перемен»